bosko
Member
Hallo,
In mein Canvas Script habe ich mir eine Rechteck erstellt.
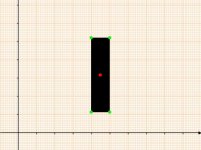
der Rote Punkt zeigt die Mitte des Objektes wo es sich Drehen soll,
hier soll die Eckpunkte (x,y,) ermittelt werden, so noch ganz leicht...
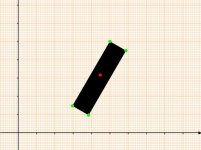
Wenn ich nun um 30Crad drehe, kann ich die leichte Berechnung von
"ecke1.x = center.xy + (breite.rechteck / 2)"
"ecke1.y = center.xy + (hoehe.rechteck / 2)"
für ein Punkt nicht mehr wirklich verwenden, wie berechnet man dies
nach einer Rotation?
Gruß
In mein Canvas Script habe ich mir eine Rechteck erstellt.

der Rote Punkt zeigt die Mitte des Objektes wo es sich Drehen soll,
hier soll die Eckpunkte (x,y,) ermittelt werden, so noch ganz leicht...

Wenn ich nun um 30Crad drehe, kann ich die leichte Berechnung von
"ecke1.x = center.xy + (breite.rechteck / 2)"
"ecke1.y = center.xy + (hoehe.rechteck / 2)"
für ein Punkt nicht mehr wirklich verwenden, wie berechnet man dies
nach einer Rotation?
Gruß

